Hindmarsh–Rose model
The Hindmarsh–Rose model of neuronal activity is aimed to study the spiking-bursting behavior of the membrane potential observed in experiments made with a single neuron. The relevant variable is the membrane potential, x(t), which is written in dimensionless units. There are two more variables, y(t) and z(t), which take into account the transport of ions across the membrane through the ion channels. The transport of sodium and potassium ions is made through fast ion channels and its rate is measured by y(t), which is called the spiking variable. The transport of other ions is made thorough slow channels, and is taken into account thorough z(t), which is called the bursting variable. Then, the Hindmarsh–Rose model has the mathematical form of a system of three nonlinear ordinary differential equations on the dimensionless dynamical variables x(t), y(t), and z(t). They read:
where
The model has six parameters: a, b, r, s, xR and I. It is very common to fix some of them and let the other to be control parameters. Usually the parameter I, which means the current that enters the neuron, is taken as a control parameter. Other control parameters used often in the literature are a, b or r, the first two modeling the working of the fast ion channels and the last one the slow ion channels, respectively. Very frequently, the parameters held fixed are s = 4 and xR = −8/5. When a or b are fixed the values given are a = 3 and b = 5. The parameter r is something of the order of 10−3, and I ranges between −10 and 10.
The third state equation:
allows a great variety of dynamic behaviors of the membrane potential, described by variable x, including unpredictable behavior, which is referred to as chaotic dynamics. This makes the Hindmarsh–Rose model very useful, because it is relatively simple and provides a good qualitative description of the many different patterns that are observed empirically.
See also
References
- Hindmarsh J. L., and Rose R. M. (1984) A model of neuronal bursting using three coupled first order differential equations. Proc. R. Soc. London, Ser. B 221:87–102.
![\begin{align}
\frac{d x}{d t} &= y%2B\phi(x)-z%2BI, \\
\frac{d y}{d t} &= \psi(x)-y, \\
\frac{d z}{d t} &= r[s(x-x_R)-z],
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/ccf2433ffe11e5bc884ee0ad3c28cc9c.png)
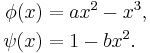
![\begin{align}
\frac{d z}{d t} &= r[s(x-x_R)-z],\\
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/7e7ffd762879ad184ef628b5c0489a9f.png)